Superdense Coding

This is a port of this notebook.

In this notebook, we use the Quantum Inspire to implement the superdense coding algorithm. With this quantum communication protocol, a sender (Bob) can transmit two classical bits of information to a receiver (Alice) using only one qubit. In addition, this method of communication is highly secure against eavesdropping since reading out the state during the communication will collapse the entangled state, indicating the presence of a third party listening.

import matplotlib.pyplot as plt
from qiskit import QuantumCircuit

from qiskit_quantuminspire.qi_provider import QIProvider

We divide the superdense code into four main sections: initilization, encoding, decoding, measurement. Initially, Alice creates the entangled state and sends one qubit to Bob for the encoding step. After the encoding, Bob returns the qubit to Alice, who decodes the message and measures the two qubits.

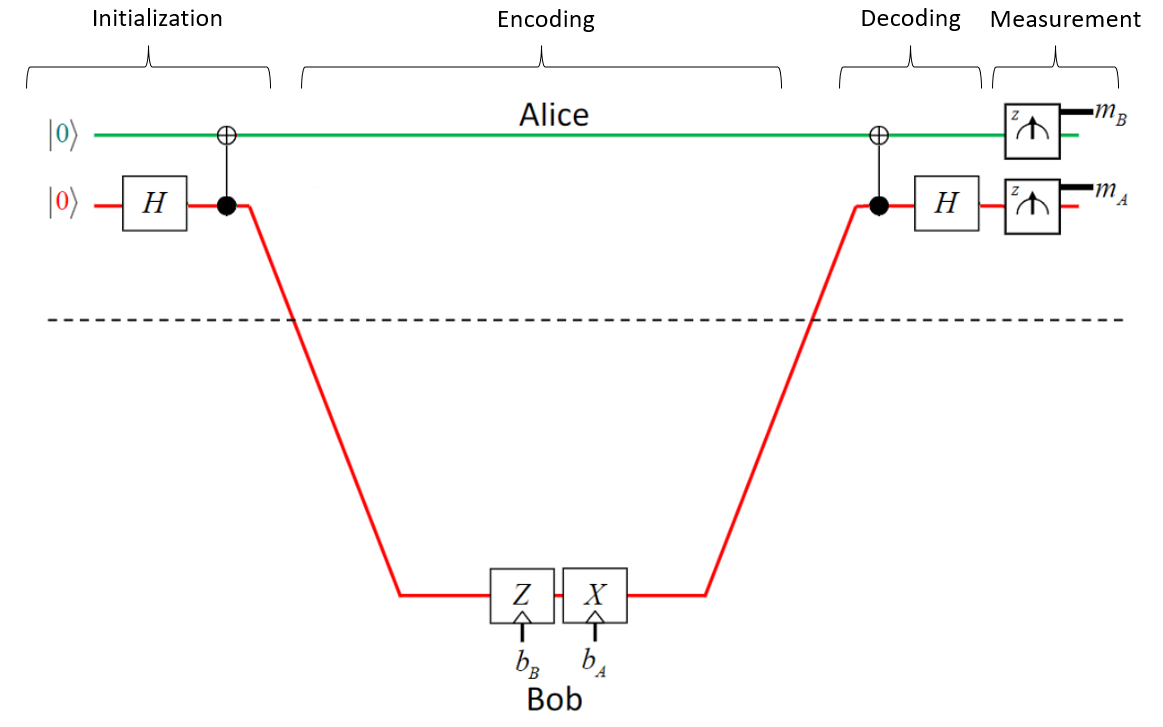
Generate the circuit

The two qubits are initially prepared in the ground state 00. Before sending the qubit to Bob, Alice needs to prepare an entangled state. So, Alice applies a H-gate followed by a CNOT-gate to obtain the desired entangled state (1/sqrt(2))(00 + 11). Now the qubit is ready to be sent to Bob, who encodes the two classical bits of information.

Bob can choose between four gates to apply to the qubit. Each gate will encode a different message for Alice. The four different possibilities are listed in the table below.

Gates	Classical Message
I	00
X	01
Z	10
ZX	11

A different Bell state will be encoded for each gate that Bob applies to the qubit. After decoding, each Bell state will result in a different 2-bit message. Remember that the Identity gate doesn’t alter the state, and the X and Z gates make the qubit do a pi-rotation over their respective axes.

The different possible states after encoding will then be:

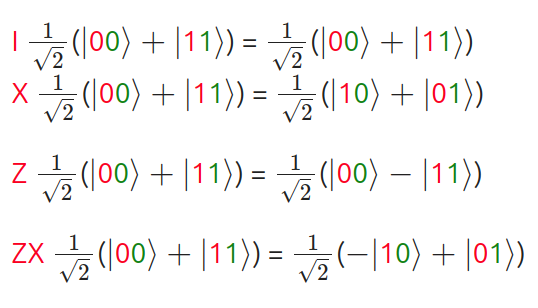
After the encoding step, Bobs sends the qubit back to Alice. To decode the message, Alice applies a CNOT-gate followed by a H-gate, as shown in the first figure. The decoding of the ‘11’ message is: H CNOT (1/sqrt(2))(-10 + 01) = 11

def superdense_encoding_circuit(bit_a: int = 0, bit_b: int = 0) -> QuantumCircuit:
    circuit = QuantumCircuit(2, 2)
    qubit_a = 0
    qubit_b = 1
    circuit.reset(qubit_a)
    circuit.reset(qubit_b)
    circuit.measure(qubit_a, qubit_a)
    circuit.measure(qubit_b, qubit_b)
    circuit.ry(1.57079632679, qubit_a)
    circuit.ry(-1.57079632679, qubit_b)
    circuit.cz(qubit_b, qubit_a)

    ## apply variable gate
    encode_gate = bit_a + 2**bit_b
    if encode_gate == 0:  # identity I
        circuit.id(qubit_a)
    elif encode_gate == 1:  # X
        circuit.x(qubit_a)
    elif encode_gate == 2:  # Z
        circuit.z(qubit_a)
    elif encode_gate == 3:  # Y
        circuit.y(qubit_a)

    circuit.cz(qubit_b, qubit_a)
    circuit.ry(-1.57079632679, qubit_a)
    circuit.ry(1.57079632679, qubit_b)

    # maximum-likelihood 3 readout (ML3 RO)
    circuit.measure(qubit_b, qubit_a)  # in qiskit this measures in z basis
    circuit.measure(qubit_b, qubit_a)  # in qiskit this measures in z basis
    circuit.measure(qubit_b, qubit_a)  # in qiskit this measures in z basis

    return circuit

Run the Circuit in Quantum Inspire Platform

We generate a circuit for each of the possibilities (00, 01, 10, 11) and then run the circuit in the Quantum Inspire. We connect and choose one of the available backends.

provider = QIProvider()
backend = provider.get_backend(name="QX emulator")

We run a job for a certain amount of shots for each combination of classical bits we wish to send. We wait for each result and collect all.

result_map = {}
for bit_a in range(2):
    for bit_b in range(2):
        circuit = superdense_encoding_circuit(bit_a, bit_b)

        # if using qxelarator
        # cqasm_string = dumps(circuit)
        # results = execute_string(cqasm_string, iterations=100).results
        # result_map[f'{bit_a}{bit_b}'] = results

        # if using thq QI2 Platform
        job = backend.run(circuit, shots=1024)
        results = job.result(wait_for_results=True)
        counts = results.data()["counts"]
        result_counts = {}
        for key in counts:
            bin_str = format(int(key, 16), "04b")
            result_counts[bin_str] = counts[key]

        result_map[f"{bit_a}{bit_b}"] = result_counts

Plot results

We plot the results of each encoding using matplotlib

fig, axs = plt.subplots(2, 2, figsize=(8, 6))
for index, key in enumerate(result_map):
    results = result_map[key]
    entries = list(results.keys())
    occurrences = list(results.values())
    i0 = int(index / 2)
    i1 = index % 2
    axs[i0][i1].bar(entries, occurrences, color="skyblue")
    axs[i0][i1].set_title(f"Supercoding {key}")
    axs[i0][i1].set_xlabel("Entries")
    axs[i0][i1].set_ylabel("Occurrences")

# Adjust layout to prevent overlap
plt.tight_layout()

# Display the plot
plt.show()